Researchers led by Michał Oszmaniec, PhD, from the Center for Theoretical Physics of the Polish Academy of Sciences have provided evidence of how the complexity of some chaotic quantum systems changes over time. They expect that their research may help us better understand what happens in black holes and wormholes.
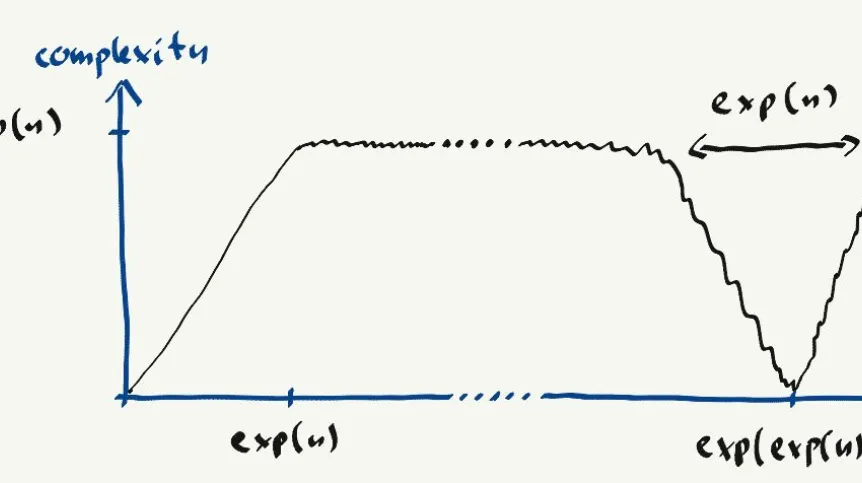
Quantum complexity means that it is difficult to recreate or describe the evolution of such systems by using simple logical operations. The state of a quantum system at a given moment can be described using a wave function. And in order to obtain such a function on a quantum computer, a certain number of simple logical operations acting on the initial state must be used. The smallest number of operations that must be used for this purpose determines the complexity of the quantum state. In chaotic quantum systems, such as random quantum circuits or strongly interacting many-body systems, this complexity changes dynamically over time: something that is relatively simple at the beginning, quickly becomes complex.
An important insight showing what happens over time to the complexity of such systems was the Brown Susskind conjecture. It suggests that the evolution of complexity in such systems consists of three stages. Initially, it grows linearly in the depth of the circuit, until a depth exponential in the system size. Then it reaches a maximum value (saturates) and remains maximally complex, until it finally returns to a small value (undergoes recurrence) at doubly exponential times.
Michał Oszmaniec explains in an interview with PAP that Leonard Susskind is one of the 'popes' of quantum physics. He creates bold conjectures, but leaves the detailed proof of them to others. 'His statements are inspiring, but he is not strict in his approach', Oszmaniec says. He adds: 'He likesprefer rigorous research, using interesting mathematical tools such as high-dimensional probability theory, group theory, and Markov processes. These techniques seemed suitable for attacking the problem posed by Brown and Susskind. My colleagues and I became interested in finding a precise proof of this conjecture'.
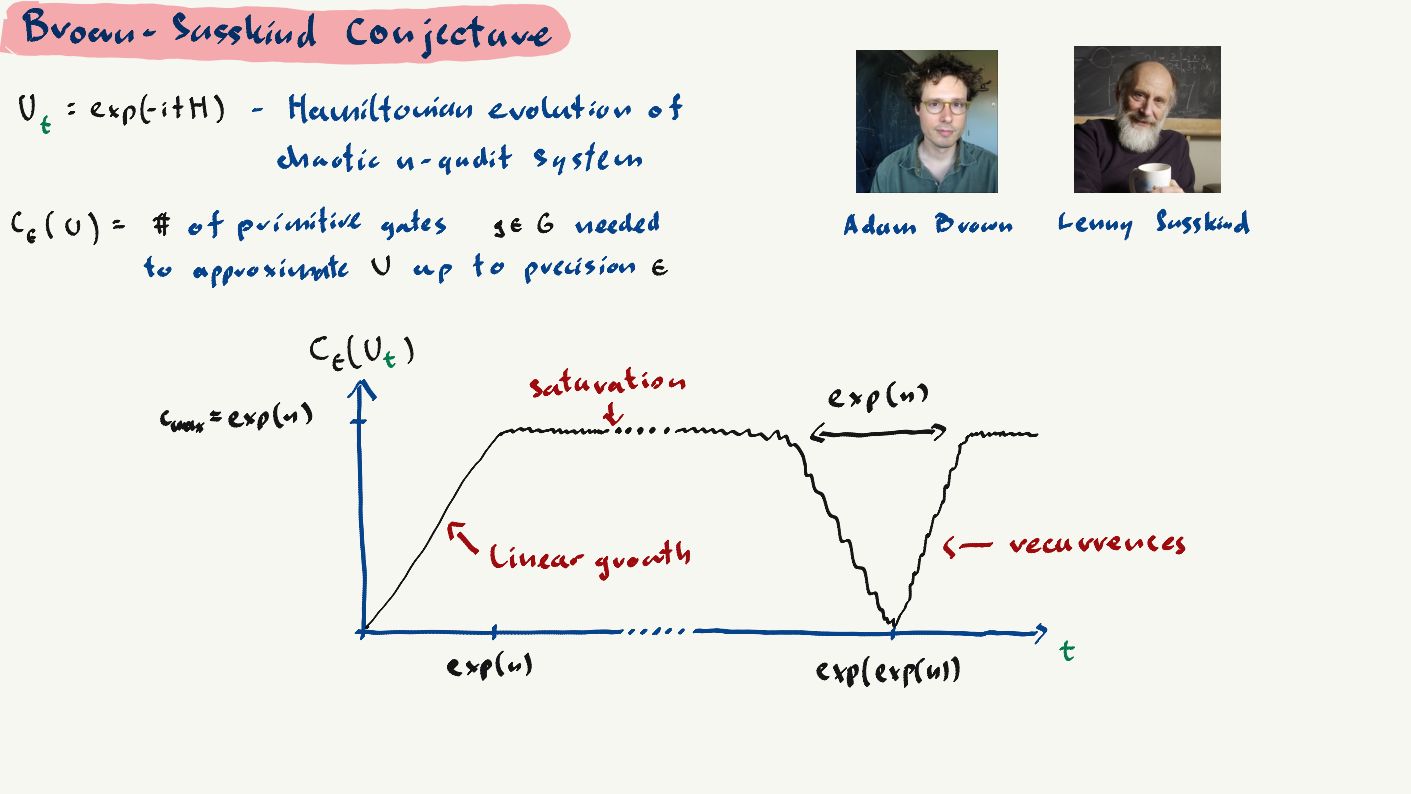
They have succeeded. The research conducted by a team of scientists from Poland and the United States (Marcin Kotowski from the Center for Theoretical Physics PAS, Michał Horodecki from the University of Gdańsk, and Nick Hunter-Jones from Stanford University also participated in the research project) provides a rigorous proof of key aspects of the conjecture in the area of complexity saturation and recurrence in a wide class of quantum models of chaotic systems. The results were described in a paper published in the prestigious Physical Review X.
'This conjecture is mentioned in the context of the theory of gravity. Part of the scientific community believes that this complexity, which is important for quantum calculations, plays an important role in black holes, and potentially - in the future theory of quantum gravity', Oszmaniec says.
The greatest dreams of physicists include combining the theory of gravity with quantum theory. One way to do this is to show that a system in the theory of gravity corresponds to a system on the side of quantum theory.
In the theory of gravity, there are quantities that grow over time. One of them is the volume of the space-time tunnel (wormhole), which connects two Anti-de Sitter spaces. Scientists have wondered what corresponds to this volume on the quantum side. One of the hypotheses is the complexity of the appropriate wave functions. It grows over a long time, and this is supposed to correspond to the volume of the wormhole.
This is a reasonable idea to combine quanta with gravity, because we have known for many years that black holes are good 'mixers' of quantum information. This is manifested, among other things, in the fact that the entanglement of states inside a black hole grows rapidly in time, reaching saturation after the time associated with the surface of the black hole. Thus, quantities such as the entanglement of states cannot correspond to the volume of a wormhole.
The scientists hope that the techniques and conclusions from their work will lead to progress in the study of complexity in more realistic chaotic quantum systems. In particular, the goal is to demonstrate similar behaviour in closed quantum systems, without constantly introducing randomness into the system. Such systems are common in many-body physics and quantum information theory. The greatest hopes for applications of quantum computers (when they are finally developed) are associated precisely with simulating such systems.
'Quantum computing is not only applied science and the hype associated with building quantum computers. It is also an interesting basic science, in which fundamental questions of the way the world works arise', comments Michał Oszmaniec. (PAP)
PAP - Science in Poland, Ludwika Tomala
lt/ bar/













