The world premiere concert of the acoustic decaphonic piano took place in July 2023, and now it was repeated in Toruń as part of the Nowe Obroty (New Revolutions) event, the final act of the Year of Nicolaus Copernicus.

TOO MANY NOTES!

A standard acoustic piano has 12 keys per octave (7 white and 5 black keys. But what if we divided the octave into a different number of parts? For a long time, jazz pianist Leszek Możdżer had the idea to check what a piano tuned to a 10-point scale would sound like. He wanted to show through music that the decimal system that we use every day, for example when counting money, is not as perfect as the duodecimal system that, in the artist's opinion, is closer to nature.

To achieve this, the pianist needed the support of scientists. By chance, he was contacted by a professional mathematician, Professor Paweł Nurowski from the Centre for Theoretical Physics at the Polish Academy of Sciences. The researcher was looking for an artist who would agree to perform at the mathematical conference 'Grieg meets Chopin'. Możdżer told him about the decaphonic piano, and the researcher agreed to help the artist prepare the instrument. Możdżer - as he recalled at the concert - then thought: 'Let the mathematicians listen to what an ugly system we live in'. Half a year later, the artist had the world's first acoustic piano tuned on a 10-step scale, or - as he called it - a decaphonic piano. Was the decimal system transferred to the world of music really that ugly and bad? Before we find out, let us try to understand Możdżer's idea.

MELODIC RELATIONSHIPS

Professor Nurowski told PAP that Możdżer wanted to calculate how to divide the octave into 10 parts, equally tempered (equally spaced) on a logarithmic scale.

The researcher explains that the brain recognizes a melody not by the specific frequencies of sounds that follow one another, but rather by the ratios of these frequencies to each other. This is why you can start singing a song with a sound at a frequency that suits you, and if you choose subsequent sounds in the same proportions as in the original, the audience should recognize the melody (such a change in key is called transposition).

One of the most characteristic ratios of sound frequencies (i.e. intervals) is the octave. If two notes differ by an octave, it means that the frequency of one note is twice as high as the other. 2:1 is an elegant proportion, so the 'lower C' harmonizes nicely with the 'upper C' (and in the case of a piano - with each subsequent C). Now the question is, what elegant proportions to divide the sounds within the octave. Pythagoras had his own way: he found nice-sounding intervals: a 3/2 fifth and a 4/3 fourth, and he derived the remaining notes in the octave - 12 in total - by combining these proportions.

ROOTS OF BEAUTY

The Pythagorean scale - although mathematically elegant - caused problems when transposing the melody (changing the key), because the intervals between the frequencies are not perfectly equal. Hence the idea for equally tempered scales. The successive parts of the octave are arranged on a geometric scale. In the case of the Pythagorean and equally tempered scales, the differences between the frequencies were insignificant from a layperson's point of view.

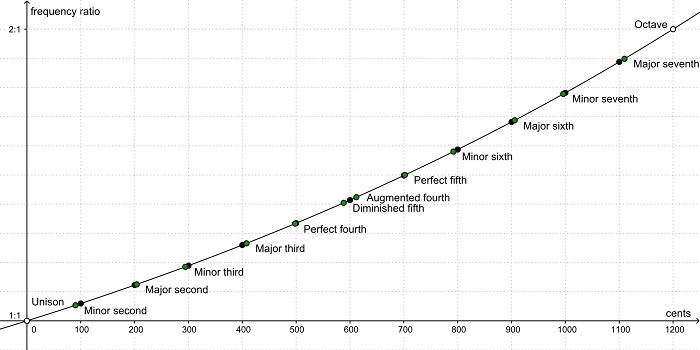
The division into equal geometric proportions within the octave can be made into any number of parts. However, for cultural reasons, a 12-step division is common.

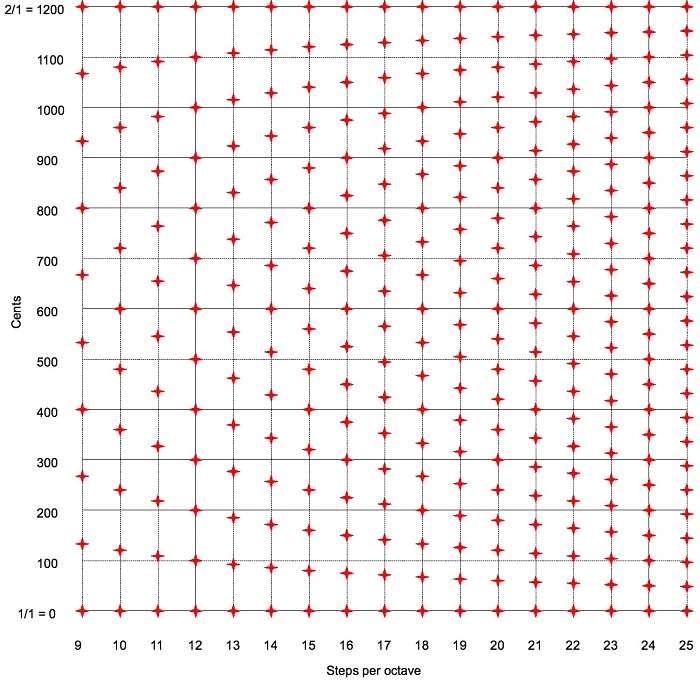
On the 12-note scale, the frequency ratios of sounds produced by successive keys are always the twelfth root of two. Meanwhile, on a 10-degree scale, the ratio of every two consecutive frequencies is the tenth root of two. Calculating successive intervals on this scale was very simple. And soon it was possible to listen to the sound of individual piano keys on an electronic simulator.

DO NOT DESTROY THE PIANO

It was clear that building a completely new decaphonic piano would be difficult and expensive. The problem was therefore how to adapt the traditional piano to the new scale. The help of a pianist and physicist, Aleksander Bogucki from the Institute of Experimental Physics at the University of Warsaw, was indispensable.

However, there were more difficult challenges that also required the support of scientists: is it possible to tune an ordinary piano to these new values without destroying the instrument?

It may seem that the easiest way would be to simply assign all the calculated sounds to subsequent keys. 'However, with this setting, the piano would be subjected to excessive stress,’ says Professor Nurowski.

Moreover, the piano keys have their own arrangement that repeats every 12 keys and - from the pianist's point of view - it is easier for analogous tones in subsequent octaves to be in the same reference place. So it was decided that two notes in each octave would be doubled.

There were several hundred possibilities of selecting these double keys. 'We checked which settings did not make sense from the point of view of the piano's construction - in which the strings would not hang too loosely or be too tightly. We ended up with about 10 combinations, which probably shouldn't destroy the device. We left the final decision to Leszek Możdżer,’ Nurowski says.

'In Leszek Możdżer's piano, we painted two surplus black keys in each octave white,’ says Mirosław Mastalerz, who tuned the piano.

THE DECIMAL SOUND

Another thing that worried the scientists was whether such an instrument would still sound like a piano. Compared to a traditional piano in a decaphonic tuning, there are only two common sounds in each octave - the consonance of which is the so-called the devil's interval, or tritone. 'The remaining eight sounds were far from what we know, so they may have sounded strange, but not terribly bad,’ Professor Nurowski.

Video: Decaphonic piano keyboard - test version. B and B and F and F sharp tuned in unison. The keys are not removed but painted white to make it easier for the pianist to play. Ultimately, the F sharp and B keys will be removed. The instrument is presented by tuner Piotr Pilzak. Credit: Mirosław Mastalerz

'A piano out of tune has a completely different sound. Here we simply had unusual sounds. After a few minutes, however, the ear would get used to them says Mirosław Mastalerz.

Why? The ratios of individual sounds on the new scale have been preserved and evenly distributed, the brain is able to perceive certain relationships between them - including melodies. So these are not randomly selected sounds, but there is a rule we know from the 12-note scale. Only the 'steps' within one octave are steeper.

10+12 = SOMETHING NEW

Możdżer drew attention to the intertwining of the decimal and duodecimal systems in everyday life. He associated the duodecimal system more with nature and metaphysics, and the decimal system - in his opinion, was more mundane and imperfect. He noticed the duodecimal systems in India when he saw the locals counting to 12 on their fingers with one hand - using their thumb to point to the successive phalanges on the four fingers of the same hand. The duodecimal system is still preserved on clock dials and in the number of months. The decimal system is commonly used, for example, in calculations of distances, weights and amounts.

'This system is beautiful in its own way,’ Możdżer said. He added that we did not yet fully recognize which intervals were consonances (pleasant to the ear) and which were dissonances (less pleasant). 'It has its good sides - you don't know what is good and what is bad,' Możdżer joked.

During his concert, the pianist played two pianos placed side by side - a classical and a decaphonic one. He demonstrated various ideas, on both a 'traditional' and a decaphonic piano. Finally, he simultaneously played two pianos. It was a reference to the intertwining of two systems in everyday life - the one associated with the earthly order and the metaphysical one. It turned out that these orders could be combined.

PHILOSOPHY (AND ECONOMICS) OF CHANCE

'This collaboration between us and Leszek Możdżer came about by chance. We should appreciate such accidents! Artists should not be underestimated. If someone comes to you with a problem, try to understand how you can help. I was the first mathematician Leszek Możdżer talked to. I wonder if history would be the same if the pianist had talked to another representative of my field. Because some people are very strict in their approach to both mathematics and music,’ says Professor Nurowski.

In his research, the scientist deals with topics in the field of mathematical physics, applications of geometry in physics and the theory of relativity. When asked if his work has anything to do with music, he answers that it does not. But who knows... Maybe it will at some point... Scientists have filed a patent application to protect the method of tuning a decaphonic piano. They reveal that there is already an idea for pianos tuned to a 19-note scale. 

***

Nowe Obroty (New Revolutions) took place on February 16-18 in Toruń. The events concerning future revolutions in science, art and society, were the final act of the Year of Nicolaus Copernicus celebrations in Toruń. The curator of Nowe Obroty was Dr. Jan Świerkowski from the B61 Institute.

PAP - Science in Poland, Ludwika Tomala

tr. RL

kap/